

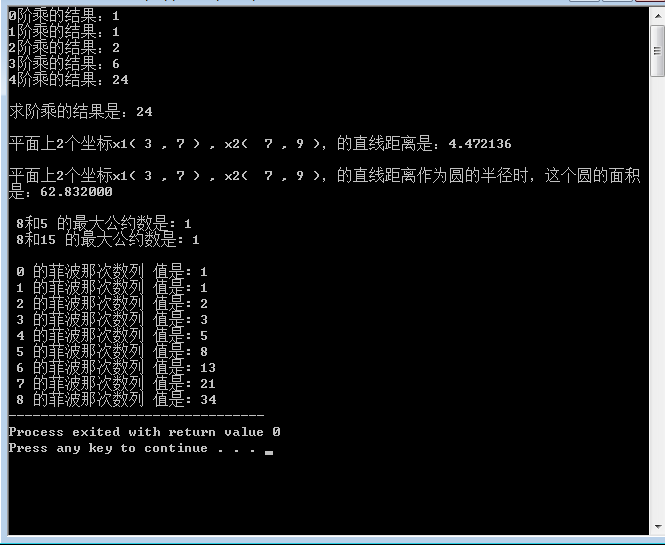
1 #include2 #include 3 #include 4 5 char explode( char * str , char symbol ); 6 7 8 double distance ( int x1 , int y1 , int x2 , int y2 ); // 求平面上2个坐标点的直线距离 9 double circle_area( double radius ); // 求圆面积。 radius 半径 10 double two_point_cacl_circle_area ( int x1 , int y1 , int x2 , int y2 );// 从两点坐标,求圆的面积 11 12 // 阶乘,递归方式实现。 13 int jiecheng( int N ); 14 15 // 递归方式,求2数的最大公约数 16 int digui_gongyueshu( int a , int b ); 17 // 菲波那次数列 18 int fibonacci( int N ); 19 20 int main( int argc , char ** argv ){ 21 char * str = "4;5;6;18;26;31;42;57;66;67;68;69;70;71;72;73;74;75;76;77;78;79;80;81;82;83;84;85;86;89;90;91;93;94;95;96;97;98;99;100;101;102;103;104;105;1051;1052;1310;1023;1041;1203;1256;1259;1260;1270;1210;1209;1279;1282;1278;1211;1276;1275;1240;1236;1235;1234;1239;1281;1028;1026;1231;1232;1277;1042;1050;1019;1267;1266;1268;1295;1265;1264;1258;1289;1219;1218;1217;1216;1016;1252;1251;1250;1249;1245;1244;1215;1243;1242;1302;1255;1287;1241;1253;1230;1271;1272;1054;1283;1284;1285;1286;"; 22 char * result = ""; 23 char list = {}; 24 int x1 = 3 , y1 = 7 , x2 = 7 , y2 = 9; // 2个坐标 25 26 printf( "\n求阶乘的结果是:%d \n" , jiecheng( 4 ) ); 27 28 printf( "\n平面上2个坐标x1( %d , %d ) , x2( %d , %d ),的直线距离是:%f \n" , x1 , y1 , x2 , y2 , distance( x1 , y1 , x2 , y2 ) ); 29 30 printf( "\n平面上2个坐标x1( %d , %d ) , x2( %d , %d ),的直线距离作为圆的半径时,这个圆的面积是:%f \n" , x1 , y1 , x2 , y2 , two_point_cacl_circle_area( x1 , y1 , x2 , y2 ) ); 31 32 33 printf( "\n 8和5 的最大公约数是: %d " , digui_gongyueshu( 8 , 5 ) ); 34 printf( "\n 8和15 的最大公约数是: %d \n" , digui_gongyueshu( 8 , 15 ) ); 35 36 int i = 0; 37 for( ; i <= 8 ; ++i ){ 38 printf( "\n %d 的菲波那次数列 值是: %d " , i , fibonacci( i ) ); 39 } 40 41 //printf( "%s \n" , str ); 42 return 0; 43 } 44 45 char explode( char * str , char symbol ){ 46 char list = {}; 47 int i = 0 , j = 0; 48 int len = strlen( str ) ; 49 // int len = sizeof( list ) / sizeof( int ); // 如果是int,float,double型, 通过sizeof()来计算list的长度 50 51 /* 52 for( ; i < len ; ++i ){ 53 if( str[ i ] != symbol ){ 54 list[ j ] += str[i]; 55 } 56 else{ 57 ++ j; 58 } 59 } 60 */ 61 62 return list; 63 } 64 65 66 67 // 通过画勾股定理直角三角形 ,求平面上2个坐标点之间的巨鹿 68 double distance ( int x1 , int y1 , int x2 , int y2 ) { 69 int x = 0 , y = 0; 70 double res = 0.0; 71 72 x = abs( x2 - x1 ); // 直角三角形的 勾 73 y = abs( y2 - y1 ); // 直角三角形的 股 74 75 res = sqrt( x * x + y * y ) ; // 勾股定理 求 斜线 76 return res; 77 } 78 79 // 求圆面积。 radius 半径 80 double circle_area( double radius ){ 81 double pi = 3.1416 ; 82 return pi * radius * radius; 83 } 84 85 // 从两点坐标,求圆的面积 86 double two_point_cacl_circle_area ( int x1 , int y1 , int x2 , int y2 ){ 87 return circle_area( distance( x1 , y1 , x2 , y2 ) ); 88 } 89 90 // 阶乘,递归方式实现。 91 int jiecheng( int N ){ 92 int res = 0 ; 93 94 // 先写1个,参数最小的情况的返回值 95 if( N == 0 ){ 96 res = 1; 97 } 98 // 再写1个递归调用的情况。 99 else{100 res = N * jiecheng( N - 1 );101 }102 printf( "%d阶乘的结果:%d \n" , N , res );103 // 完成递归。 104 return res;105 106 /*107 我们从数学上严格证明一下factorial函数的正确性。108 刚才说了,factorial(n)的正确性依赖于factorial(n-1)的正确性,109 只要后者正确,在后者的结果上乘个n返回这一步显然也没有疑问,那么我们的函数实现就是正确的。110 111 因此要证明factorial(n)的正确性就是要证明factorial(n-1)的正确性,112 同理,要证明factorial(n-1)的正确性就是要证明factorial(n-2)的正确性,113 114 依此类推下去,最后是:要证明factorial(1)的正确性就是要证明factorial(0)的正确性。115 116 117 而factorial(0)的正确性不依赖于别的函数,它就是程序中的一个小的分支return 1;,118 这个1是我们根据阶乘的定义写的,肯定是正确的,因此factorial(1)也正确,119 因此factorial(2)也正确,120 依此类推,最后factorial(n)也是正确的。121 122 其实这就是中学时讲的数学归纳法(Mathematical Induction),123 用数学归纳法来证明只需要证明两点:Base Case正确,递推关系正确。 124 */125 }126 127 128 // 递归方式,求2数的最大公约数 129 int digui_gongyueshu( int a , int b ){130 int res = 0 ;131 if( a % b == 0 ){132 res = b;133 }134 else{135 res = digui_gongyueshu( b , a % b );136 }137 return res;138 139 /*140 1、编写递归函数求两个正整数a和b的最大公约数(GCD,Greatest Common Divisor),使用Euclid算法:141 142 1. 如果a除以b能整除,则最大公约数是b。143 2.否则,最大公约数等于b和a%b的最大公约数。144 145 Euclid算法是很容易证明的,请读者自己证明一下为什么这么算就能算出最大公约数。 146 */147 }148 149 // 菲波那次数列 150 int fibonacci( int N ){151 int res = 0 ;152 153 if( N == 1 || N == 0 ){154 res = 1;155 }156 else{157 res = fibonacci( N - 1 ) + fibonacci( N - 2 );158 }159 return res;160 }161 162
c语言求平面上2个坐标点的直线距离、求俩坐标直线距离作为半径的圆的面积、递归、菲波那次数列、explode